- Resolver ecuaciones de tercer grado o mayor (cuarto grado, quinto grado …)
- Dividir un polinomio entre un binomio que sea de la forma x-a
- Factorizar polinomios de tercer grado o mayor (cuarto grado, quinto grado …)
- Calcular las raíces de polinomios de grado mayor o igual a 3
Con la regla de Ruffini, solamente se obtienen las soluciones enteras. Si la ecuación tiene soluciones complejas o reales, éste método no es válido.
Veremos que para obtener las soluciones de la ecuación, previamente hay que factorizar, por lo que con el mismo ejemplo explicaremos ambos conceptos.
Vamos a resolver un ejemplo explicando paso por paso.
Tenemos la siguiente ecuación:

1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:

2 – Trazamos dos líneas perpendiculares de esta forma:
 3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:
3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.
Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:

4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.
Ese número corresponde al número (a) del binomio x – a:
Ese número corresponde al número (a) del binomio x – a:

En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini

5 – Empezamos a ejecutar el método. El primer hueco de la segunda fila, siempre se deja libre:

6 – Se hace la suma de la primera columna y el resultado de pone abajo:

7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:

8 – Se realiza la suma de la segunda columna:
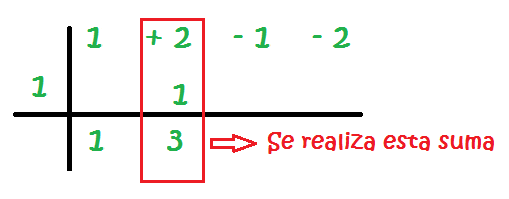
9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:

10 – Así sucesivamente hasta completar todas las columnas:
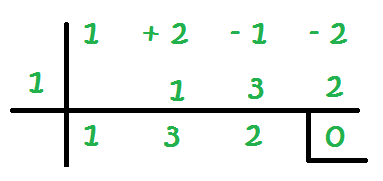
El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:

Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.
No hay comentarios:
Publicar un comentario