REGLAS DE DIVISIBILIDAD DEL 2 ,4 , 8 , 3 , 6 , 25 , 7

2= Cuando su última cifra es par
4= Cuando las dos últimas cifras son divisibles por 4
8= Cuando la tres últimas cifras son divisores de 8 y se pueden dividir tres veces por 2
3= Cuando la suma de su cifras es múltiplo de 3
6= Cuando acaba en par y la suma de sus cifras tiene que ser múltiplo de 3
11= Ejemplo: 528    5 +8 = 13  13-2=11          se suman el 5 y el 8 y se resta 2 al resultado y da 11
25= Si termina en 25 , 50 , 75 , 00 , es múltiplo de 25
7= Se múltiplica su última cifra por 5 y luego el resultado que de , se le suma las dos primeras cifras .
Ejemplo = 119    9x5=45   45 +11=56  que es múltiplo de 7

¿Cómo averiguar la letra de un DNI?

Para obtener la letra del DNI solo hay que dividir el número entre 23 y el número resultante del resto de esta división hay que buscarlo en la siguiente lista que nos indicará que letra le corresponde:

0 T   5 M   10 X   15 S   20 C
1 R   6 Y   11 B   16 Q   21 K
2 W   7 F   12 N   17 V   22 E
3 A   8 P   13 J   18 H   
4 G   9 D   14 Z   19 L 

Por ejemplo al número de DNI 12345678 al dividirlo entre 23 el resultado es 536768 y resto 14. En la lista se puede comprobar que al número 14 le corresponde la letra Z. Por lo que este DNI con letra incluida sería 12345678Z.

REGLAS DE DIVISIBILIDAD DEL NÚMERO 13 , 17 ,19 Y 23

13= Cuando separando la primera cifra de la derecha , multiplicándola  por 9 restando este producto de lo que queda a la izquierda y así sucesivamente da 0 o múltiplo de 13.
17= cuando separando la primera cifra de la derecha , multiplicándola por 5 , restando este producto de lo que queda a la izquierda y así sucesivamente da 0 o múltiplo de 17.
19= Cuando separando la primera cifra de la derecha , multiplicándola por 2 , sumando este producto de lo que queda a la izquierda y así sucesivamente da 19.
23= Cuando le quitamos o retiramos su última cifra , la suma  del número resultante y 7 veces esa última cifra es 0 o múltiplo de 23.

ERRORES DEL GUIÓN

-Cuando  Lorena habla de los criterios de divisibilidad dice que 

Un número es divisible por 19 cuando separando la primera cifra de la derecha, multiplicándola por 17, restando este producto de lo que queda a la izquierda y así sucesivamente, da cero o múltiplo de19.

*hay que multiplicar la primera cifra por 2 no por 17, y sumando este producto de lo que queda a la izquierda y así sucesivamente, da 19 

-y cuando dice 

Un número es divisible por 11 cuando la diferencia entre la suma de los valores absolutos de sus cifras de lugar impar y la suma de los valores absolutos de sus cifras de lugar par, de derecha a izquierda, es cero o múltiplo de 11.

*corrección con un ejemplo: 

528: se suman el 5 y el 8 y se resta con el 2 que es el del medio y nos da 11

 - En el minuto 6:41 Lorena dice que los divisores encontrados hasta ahora son 1, 2, 4, 28 y 56, sin embargo, no menciona el 112, que también lo es como ha demostrado Femili anteriormente.

¿Qué son las congruencias en Z + Módulo M ?

Definición de congruencia

Dado m ∈ Z , m> 1, se dice que a, b ∈ Z son congruentes módulo m si y sólo si m|(a-b). Se denota esta relación como a ≡ b (mod m). m es el módulo de la congruencia.

Es importante darse cuenta de que si m divide a a-b, esto supone que ambos a y b tienen el mismo resto al ser divididos por el módulo m.

Ejemplos: 23≡2 mod 7 (porque 23=3.7 + 2), y -6≡1 mod 7 (porque -6= -7.1 +1)

La relación de congruencia como equivalencia. El conjunto de residuos.

La relación de congruencia módulo m es una relación de equivalencia para todo m ∈ Z. Es decir, cumple las propiedades reflexiva, simétrica y transitiva. Como en toda relación de equivalencia, podemos definir el conjunto cociente de las clases de equivalencia originadas por la relación de congruencia. En este caso la relación clasifica a cualquier entero a según el resto obtenido al dividirlo por el módulo m.

Llamaremos Z_m al conjunto cociente de Z respecto de la relación de congruencia módulo m. A la clase de equivalencia de un elemento a ∈ Z se la denota por [a]_m o simplemente [a].

Para todo a∈Z se tiene que [a] = [r] en Z_m, donde r es el resto de dividir a entre m.Por lo tanto, el conjunto Z_m es finito y tiene m elementos: Z_m = { [0]_m, [1]_m, ... , [m-1]_m}, donde la clase [i]_m representa al conjunto de todos los enteros que son congruentes con i mod m. A este conjunto cociente se le conoce como el conjunto de restos o residuos (módulo m)

Ejemplo: siguiendo con el ejemplo anterior, está claro que en Z₇, el número entero 9, el 16 y el 23 pertenecen todos a la clase [2], y que el entero -6, el 1 y el 8 pertenecen a la clase [1]

Compatibilidad de la relación de congruencia con la suma y el producto

Sean m ∈ N y a, b, c, d ∈ Z tales que a ≡ b (mod m) y c ≡ d (mod m). Entonces se cumple que:

1. a + c ≡ b + d (mod m)
2. a . c ≡ b . d (mod m)

Consecuentemente, el resto de la suma es congruente con la suma de restos, y el resto del producto es congruente con el producto de restos. Además podremos sumar y multiplicar clases de equivalencia (residuos) porque es indiferente el representante que se elija de cada clase a la hora de operar: el resultante de la operación siempre será un representante de la misma clase resultado.

Vamos ahora a definir la aritmética módulo m o aritmética en Z_m:

Estadística descriptiva

Conceptos básicos

* Población: conjunto
* Individuos: elementos
* Tamaño de la población: número de elementos
* Características o variables estadísticas:

• Cualitativas
• Cuantitativas
• Discretas
• Continuas
• recuento de datos : tabla de frecuencias

Graficos estadísticos 

Parámetros estadísticos

• De posición
• Media
• Mediana
• Moda
• De dispersión
• Desviación media:la desviacion  respecto a la medida da información de lo alejado o cerca que está un dato de los demás datos del conjunto
• Varianza
• Desviación típica o estándar

Áreas y volumenes de cuerpos geométricos

Ángulos en la circunferencia

Teorema de Tales

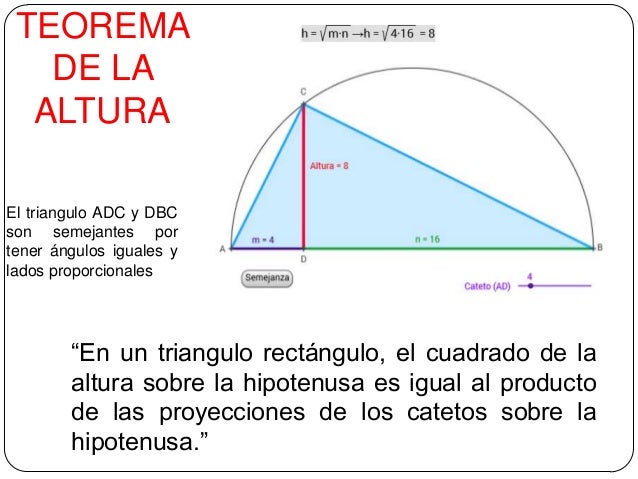
Teorema de pitágoras

Teorema de Pitágoras 

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

     

Teorema de la altura

Teorema de los catetos

Teorema del cateto

Explotación en los paises pobres ¿quiénes ?

Los países ricos explotan  a los países pobres, tanto a sus recursos como a las personas.

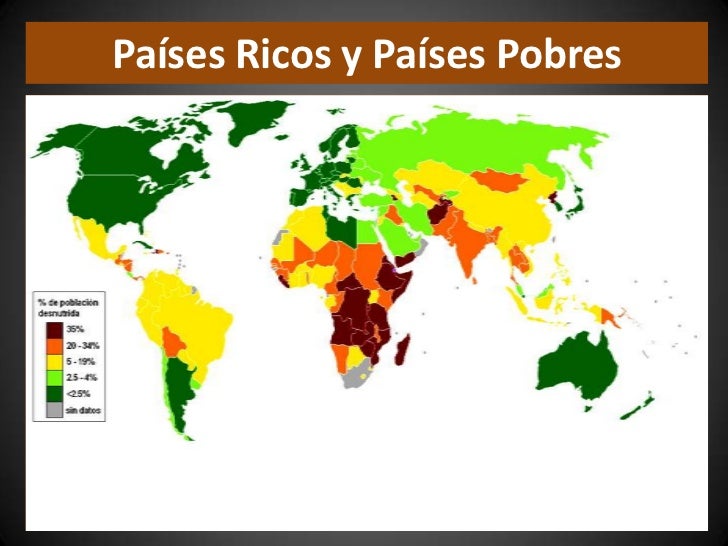
La explotación de los países ricos a países pobres, no es justificable aunque muchos piensen que es legítima, vivimos en el mismo planeta y deberían existir derechos universales para cada persona, donde cada decisión tomada por las grandes instituciones europeas o americanas tenga un carácter global encaminado al desarrollo. No es posible que en pleno siglo XXI siga existiendo explotación, pobreza, hambre y millones de muertes inocentes, de hombres que por tener la suerte de nacer en un país pobre, sin oportunidades, padecen y mueren en estas condiciones.

Sin embargo muchos de los países más pobres del mundo tienen grandes reservas de materias primas, pero les falta la tecnología y los inventos de los países ricos. Muchos expertos piensan que este es uno de los principales motivos de la diferencia de riqueza entre unos países y otros, pero también es verdad que el desarrollo de los países ricos ha sido por la explotación y expoliación de los pobres. La compra de esta tecnología por parte de estos países les es muy costosa, pues les hace dependientes tanto económica como tecnológicamente obligándoles a un sometimiento también político.

DISEÑOS SOCIALES POSITIVOS QUE FACILITAN LA VIDA EN LOS PAISES POBRES

 

· LifeStraw: es un dispositivo que filtra el 99% de las bacterias y el 98% de los virus que se encuentran en aguas contaminadas. Existe también una versión “familiar” que filtra agua continuamente. Funciona con una serie de filtros de diferentes tamaños, resina con yodo y carbón activado para absorber agentes tóxicos. Es tan efectivo como cualquier otro filtro de agua o hervirla. Se supone que cada uno de estos productos permite ingerir hasta 700 litros de agua. Su costo es de $2.

Hippo Rollers: Una especie de bidones hechos con la idea es facilitar la carga de agua desde pozos o ríos en comunidades en las cuales el acceso a este recurso es difícil y requiere mucho tiempo y esfuerzo.

Catastrofe ecológica

Una catástrofe ecológica es una desgracia que ocurre cuando, por causas naturales (un tsunami, un volcán, un tornado) o por causas humanas (un derrame de petróleo en el mar, contaminación de los ríos) se provoca un deterioro del paisaje, muerte, enfermedades etc..., perjudicando el medio ambiente, fauna, flora y seres humanos.

Los desastres pueden ser originados por diferentes motivos:

Los desastres pueden ser originados por diferentes motivos:

·         Desastres generados por procesos dinámicos en el interior de la Tierra: Sismos,
Maremoto, Erupciones volcánicas

  ·         Desastres generados por procesos dinámicos la superior de la Tierra: Deslizamientos de las tierras, Derrumbes, Aludes, Aluviones.

·         Desastres generados por los fenómenos meteorológicos o hidrológicos: Inundaciones, Sequías, Heladas, Tormentas, Granizadas, Tornados, Huracanes.

·         Desastres de origen biológico: Plagas, Epidemias